Három ókori geometriai probléma

A kör négyszögesítése

A probléma az időszámításunk kezdete előtti VI. század táján a kör területének kiszámításánál merült fel az ókori görögöknél. A megoldáshoz egy képletre volt szükség, annak a négyszögnek a megrajzolásához, amelynek a területe pontosan megfelel egy adott kör területének.

A feladat euklideszi szerkesztéssel nem oldható meg. Ezt az ókorban is sejtették, de csak 1882-ben bizonyította be Ferdinand von Lindemann német matematikus, hogy a π szám transzcendens, vagyis nem gyöke semmilyen racionális együtthatójú polinomiális egyenletnek. Néhány évtizeddel korábban ismert volt, hogy amennyiben a π irracionális, akkor a kör négyszögesítése euklideszi szerkesztéssel lehetetlen.


Az ókori egyiptomiak megoldása közel járt a megoldáshoz. A Rhind-papiruszban (i. e. 2000 k.) közölt legkorábbi megoldás próbálkozás eredménye. Egy 9 egységnyi átmérőjű kör területe majdnem megegyezik egy 8 egységnyi oldalhosszúságú négyzetével.

Az ókori görög matematikusok igen sok szellemes nemeuklideszi szerkesztést találtak ki. Az első eredményeket Hippokratész érte el. Számos, körívekkel határolt síkidomot (pl. Hippokratész holdacskái) alakított át ugyanolyan területű négyszöggé.

Deinosztratosz a Hippiász által feltalált triszektrix (kvadratrix) görbét használta fel a körkerület megszerkesztésére.

Arkhimédész a róla elnevezett spirális segítségével szerkesztette meg a körkerületet, amelynek ismeretében a négyszögesítés már megoldható, hiszen az "r" sugarú kör területe megegyezik annak a háromszögnek a területével, amelynek alapja a kör kerülete, magassága pedig a kör sugara. Persze sem Deinosztratosz, sem Arkhimédész szerkesztése nem euklideszi, mert a segítségül hívott görbék euklideszi módon nem szerkeszthetõk meg…

Euklideszi szerkesztéssel azonban számos jó közelítõ szerkesztés született. Ezek közül talán a legismertebb Kochanski szerkesztése. A félkör kerületét, négy tizedes pontossággal szerkesztette meg.

Szerkesztésének leírása:

Rajzoljunk OA =1 sugarú kört és ennek egyik átmérõjét, AB-t. Az átmérõ B végpontjához rajzoljunk érintõ egyenest, és ebbõl a végpontból mérjük fel a BC=OA húrt.

A BC húr felező merőlegese kimetszi az érintőn a D pontot. A D pontból az érintőre, a B érintőpont felé indulva, mérjük fel a DE = 3 OA távolságot.

Végül húzzuk meg az EA szakaszt. A Pitagorasz-tételnél többet nem kívánó számítással belátható, hogy AE ~ 3,14153...

A kockakettőzés

A kocka megduplázása – az ún. déloszi probléma – egyike az antik görög matematikusok által vizsgált és megoldatlan geometriai szerkesztési feladatoknak.

Eszerint egy olyan kocka élét kellene megszerkeszteni, amelynek térfogata kétszerese egy adott kocka térfogatának. (E térbeli szerkesztés síkbeli rokona a négyzet megduplázása, ami euklideszi szerkesztéssel megoldható, azonban a kocka kétszerezése nem.)

Több ókori forrás is beszámol arról a mondáról, ami a problémát Délosz lakóihoz köti. Eszerint a délosziak Apollón Delphoiban működő jósdájához fordultak, amikor városukat a pestis megtámadta. Apollón kocka alakú oltárát kellett volna kétszeresére cserélni, hogy a járványtól megszabaduljanak.

A feladatot az a kikötés teszi megoldhatatlanná, hogy a szerkesztéshez csak körzőt és vonalzót szabad használni (euklideszi szerkesztés). A megoldás keresésében szinte minden neves ókori matematikus részt vett.

Dioklész (i. e. III. sz.) munkáit csak hivatkozásokból ismerjük. Eutokiosz az Arkhimédész-kommentárjában írta le két nevezetes szerkesztését, köztük a déloszi probléma megoldásához „felfedezett” cisszoiszt. A szerkesztés a cisszoisz megrajzolásával kezdődik. A kör sugara a megduplázandó kocka éle: a. A szerkesztés további lépéseihez csak egy vonalzó kell.

A probléma nagymértékben gyakorlati jellegű, mivel összefügg a folyadékok és a gabona mérésére alkalmas szabványeszközök megalkotásával. A Parthenon felépítésében is kulcsfontosságú szerepe volt, a templom térfogata ugyanis az előző temploménak a kétszerese.

Szögharmadolás

Az antik matematika történetében a probléma első nyomait az éliszi filozófus Hippiásznál (i. e. 420 k.) találjuk, bár maga a mű elveszett, csupán más szerzők (Proklosz, Papposz 4. sz.) hivatkozásaiból ismerjük. Bizonyára ez is, mint oly sok más téma, még ennél is korábbi eredetű. A megoldhatatlanságát az ókorban már sejtették, de bizonyítása csak az újkori matematikusoknak sikerült. A görög, arab és később az európai matematikusok az euklideszi szerkesztésekhez nem tartozó eszközöket és síkgörbéket használtak a megoldáshoz.

Hippiász (i. e. 420 k.) az elsőként ismert megoldásban az általa felfedezett speciális görbét, a quadtratrixot használja. A polárkoordinátákban egyenletű görbe pontjainak ordinátája 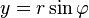arányos lévén a azimuttal, tehát a szerkesztés ennek a szakasznak az egyenlő részekre osztásával történik. Ebből következik, hogy a görbe egy szög tetszőleges számú egyenlő, vagy akármilyen arányú felosztására is alkalmazható.